Función inversa
En Matematicas, si f es una aplicación o Función que lleva elementos de I en elementos de J, en ciertas condiciones será posible definir la aplicación f -1 que realice el camino de vuelta de J a I. En ese caso diremos que f -1 es la aplicación inversa o recíproca de f.
Sea f una Función real biyectiva cuyo dominio sea el conjunto I, es decir, creciente o decreciente en el conjunto I, y cuya imagen sea el conjunto J. Entonces, la función recíproca o inversa de f, denotada f -1, es la función de dominio J e imagen Idefinida por la siguiente regla:

Destaquemos que f -1, al igual que f, es una aplicación biyectiva, que queda determinada de modo único por f y que cumple:
-
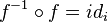 y
y -
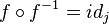 .
.
De hecho, estas dos últimas propiedades caracterizan a la función inversa, como muestra la siguiente definición alternativa.
