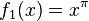Trascendentes

Una función trascendente es una función que no satisface una ecuación polinómica cuyos coeficientes sean a su vez polinomios; esto contrasta con lasfunciones algebraicas, las cuales satisfacen dicha ecuación. En otras palabras, una función trascendente es una función que trasciende al álgebra en el sentido que no puede ser expresada en términos de una secuencia finita de operaciones algebraicas de suma, resta y extracción de raíces. Una función de una variable es trascendente si es independiente en un sentido algebraico de dicha variable.